音频基础知识——音频失真是怎么回事?
我们花了很多时间思考和谈论音频中的失真，甚至有时会听到它，但它到底是什么，为什么它很重要？

音频中的失真通常有两种类型的失真：

频率失真——由带宽不足和带宽限制之间的非平坦频率响应引起

非线性失真——由硬件中的非线性引起。

这篇文章是关于非线性失真的，因为如今频率失真在现代设备中很少成为问题。非线性失真常常被错误地称为 "非线性失真"。然而，失真不是非线性的，是硬件设备的非线性

正弦波——音频信号的组成部分
这里从只有一个频率正弦波信号（图 1）讲起。在音频频率上，该正弦波被听到为单音。

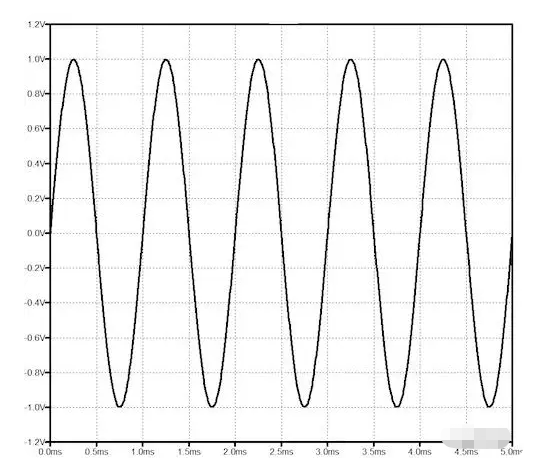
正弦波是由多种形式的自然振动或振荡产生的。考虑时钟的摆轮，它有一个水平轴。如果我们在车轮的边缘做一个标记，从侧面看，标记的高度在轴的上方(和下方)划出了一个时间上的正正波。

非线性造成音频失真
现在，无论输入波形是什么，它都可以被认为是许多正弦波的总和，输出波形也可以。尽管如此，由于波形不同，输出波形包括输入波形中没有的正弦波成分，造成了信号是失真。

对于输入信号的每个正弦波分量（称为基波），非线性产生的信号是该分量频率的倍数，称为谐波。双频称为二次谐波或二阶谐波。三倍频称为三次谐波。这些新信号是谐波失真分量。

图 2 显示了来自一个非常糟糕的电路的输入和输出信号，该电路产生 20%幅度的二次谐波和 10% 的三次谐波。将二次和三次谐波信号添加到输出会使信号失真，使其不再是纯正弦波。选择这些高失真数字是为了清楚地显示效果。

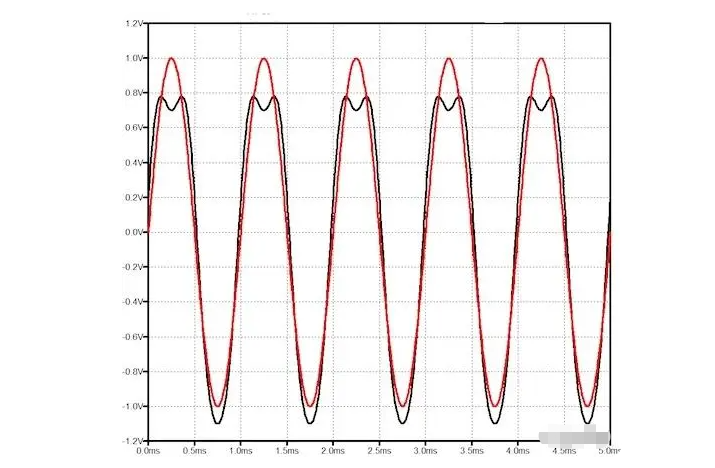
二次谐波总是导致正半周与负半周的形状不同。在本例中，三次谐波影响信号的峰值。那是因为我选择了三次谐波相对于基波相位角的相位角来做到这一点。不同的相位角会导致不同的形状变化。

乐器中的谐波示例
几乎所有乐器（和人声）产生的声音都包含许多谐波。例如，正弦波由陶笛产生，这是一种类似于口琴的小型手持管乐器，顾名思义，它会在每个音符中产生大量谐波。

添加更多谐波会改变音符的音调或音色。除非添加量很大，否则任何人通常都很难察觉差异，除非他们能够区分 Stradivarius 的声音和 Guarneri 的声音。

图 3 显示了小提琴的“谐波频谱”。频谱通常是功率或电压与频率的关系图。

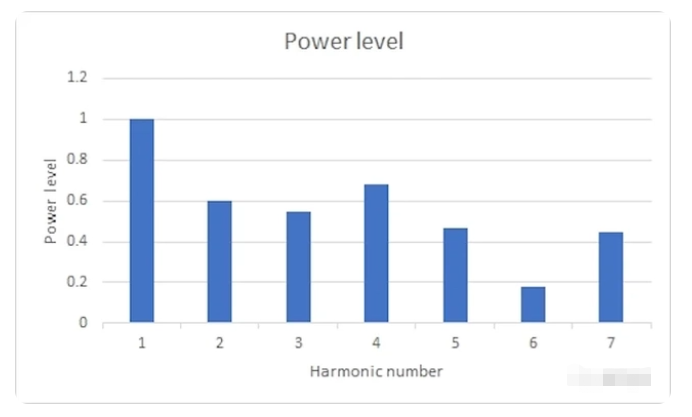
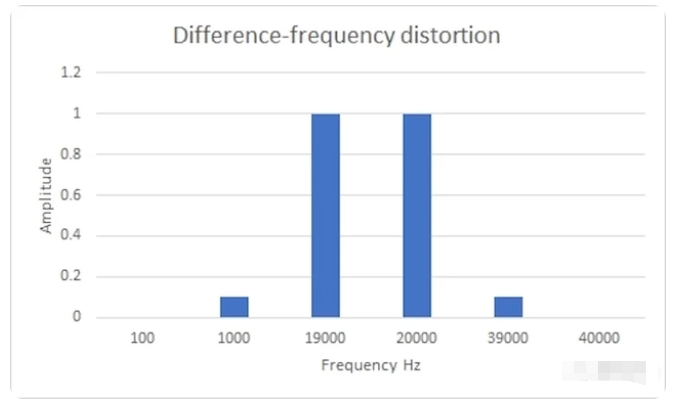
调制失真使用低频信号和更低电压的更高频率信号，通常是其他信号的四分之一。例如，信号可能是 80 Hz 和 5kHz。如图 5 所示，非线性再次产生了两个新的输出失真信号分量：

1. 4920 Hz 处的差分信号 (5000 - 80 = 4920)
2. 5080 Hz 的和信号 (5000 + 80 = 5080)

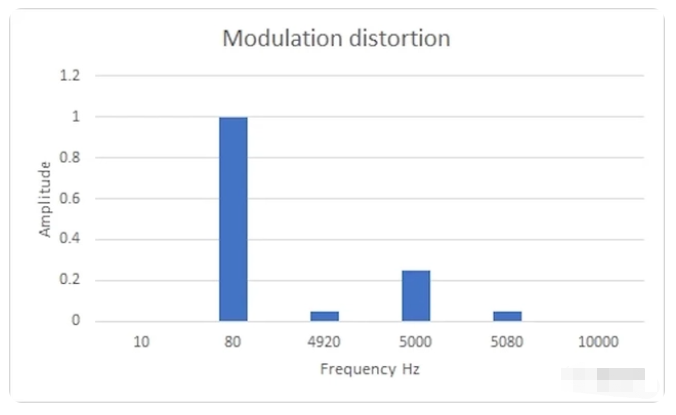
也可以测量由输入信号分量的谐波产生的其他互调分量。例如，如果我们有两个输入频率 f1 和 f2，则在 2f1 ± f2 和 2f2 ± f1 处存在互调分量，以及我们已经看到的 f1 –f2 和 f1 + f2。但是这些并没有告诉我们更多关于被测量设备的性能。

我们应该得出的结论是，我们应该消除所有非线性源，以免损坏再现的声音。然而，我们必须在放大器中使用的器件，即晶体管（，本质上是非线性的，因此我们必须使用精心挑选的设计技术来尽可能减少非线性。

这常常引发一个问题，“多少才够？” 发烧友经常就人类听觉的灵敏度和我们实际听到的失真程度争论这个问题。但是，对于这篇文章来说，这个话题太大了。文章来源网络，侵删。